Redstone : Les portes logiques
Les portes logiques sont la clef vers l'utilisation avancée de la redstone, cependant elles mettent en œuvre des principes d'électronique qui peuvent rebuter.
Si vous souhaitez vous lancer au plus vite dans la conception de circuits, d'après la base d'exemple, nous vous invitons à sauter cet article pour le moment. Nul besoin de comprendre le fond de la redstone pour réaliser vos premiers circuits ou automatisations.
Si vous avez l'âme d'un architecte en herbe ou d'un savant fou, la vraie nature de la redstone va vous être révélée ici...
Les portes logiques
Les portes logiques sont la représentation matérielle d'une fonction logique, qui agit comme un test d'état simple. Il n'existe que 2 états : vrai ou faux, que l'on peut généralement transcrire en "allumé" ou "éteint".
L'application la plus simple serait une lampe reliée à un interrupteur. Si l'interrupteur est sur off, la lampe sera éteinte. Dans le cas contraire, l'interrupteur sur "on" commande l'allumage de la lampe.
Notre fonction logique admet donc une entrée : l'interrupteur, et une sortie : la lampe. Entre les deux se situe notre fonction.
L'affaire se complique si l'on fait intervenir plusieurs "entrées", et plusieurs "sorties". Les portes peuvent être transcrites sous forme d'une formule mathématique, avec quelques symboles particulier. On utilisera en notation générale, "A", "B", "C" comme entrées, et "O" (output) en sortie.
Exemple :
A ⊽ B ⊽ C = A ⊽ ¬(B ∨ C) = O
Qui se retranscrit en "A non-ou B non-ou C = A non-ou inverse(B ou C) = O "
Les symboles des portes sont détaillés dans les paragraphes relatifs à ces portes.
La représentation simplifiée des circuits de redstone
Dans un but de clarification et de compréhension des autres guides sur la redstone, nous allons utiliser le système international de traçage de circuit en redstone :


Les circuits se font généralement sur 3 étages. Le blanc correspond à l'étage de base, le jaune au premier étage, et le gris au 3ème étage.
Le "Pont" est un circuit de redstone au Rez de chaussée, avec un circuit perpendiculaire au 3ème étage.
Les portes logiques peuvent être définies de plusieurs façons, mais dans un soucis de simplification on ne verra qu'un seul exemple par type de porte.
Les portes logiques de base
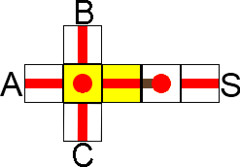
NOT (inverseur) (¬)
La porte NOT est la porte la plus simple. Elle agit uniquement en inversant le signal. Si en entrée le signal est actif, en sortie le signal sera inactif. Son principal usage est le pilotage des torches en redstone, qui requièrent un signal nul pour éclairer.
C'est une construction de base que l'on retrouvera en tant qu'élément dans nombre d'autres portes.
Table de vérité :
| A | S | |
| 0 | 1 | |
| 1 | 0 |
Schéma :
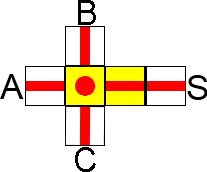
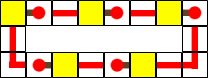
OR (ou) (∨)
La première fonction à plusieurs entrées. Si au moins une des entrées est active, la sortie est active. C'est-à-dire que si toutes les entrées sont actives, la sortie le sera aussi. Ce dernier point fait la différence par rapport à une porte XOR, ou exclusif.
Table de vérité :
| A | B | C | S | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
Schéma :
Toutes les entrées ne sont pas obligatoirement raccordées à un circuit. Pour faire une OR sur cinq entrées il faudra deux portes OR avec la sortie de la première raccordée à une entrée de la seconde.
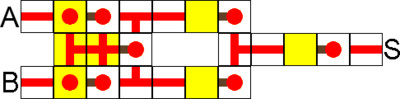
NOR (non ou) (⊽)
Il s'agit de la combinaison d'une porte OR et d'une NOT. La porte sera active que si toutes les entrées sont inactives, et seulement dans ce cas.
Table de vérité :
| A | B | C | S | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 |
Schéma :
AND (et) (∧)
Une porte qui ne s'active que si toutes les entrées sont actives.
Table de vérité :
| A | B | S | |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Schéma :
NAND (non et) (⊼)
Cette porte est l'inverse de la AND, et comme son nom l'indique c'est une AND avec une NOT à la sortie. Mais il est possible de comprimer cette porte en ce schéma (dans le cas contraire nous ferions une NOT d'une NOT, donc rien du tout).
Table de vérité :
| A | B | S | |
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Schéma :
XOR (ou exclusif) (⊻)
La porte XOR est une dérivée de la porte OR. Elle fonctionne de façon similaire, mais renvoie un signal nul si les deux entrées sont actives en même temps. C'est à dire qu'il faut que les entrées soient différentes.
Table de vérité :
| A | B | S | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Schéma :
XNOR (non ou exclusif) (≡)
La dernière des portes de base, elle renvoie un signal si les entrées sont dans des états identiques, tout à 0 ou tout à 1.
Table de vérité :
| A | B | S | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Schéma :
Les portes logiques avancées
Ce sont des portes avancées dans le sens où l'on induit une variable temporelle dans leur fonctionnement. On parle alors de bascules, et non plus de portes logiques.
Ces portes vont être non plus sensibles aux états, mais aux variations d'état. Leur usage secondaire est de fonctionner en tant que mémoire. Par exemple pour mémoriser une impulsion de bouton. Un bouton poussoir plus une mémoire donne l'équivalent d'un levier.
/!\ À noter que ces portes ont des fonctionnements "interdits". Pour certaines combinaisons d'entrées, l'état de la sortie ne peux pas être prévisible. Ils convient donc de s'assurer de ne pas laisser la possibilité d'avoir entrée une combinaison entrainant une sortie imprévisible.
On différenciera deux types de bascules :
Les synchrones, ou la sortie dépend à tout instant de l'état simultané des entrées.
Les asynchrones, ou la sortie dépendra des entrées, mais ne pourra changer d'état qu'en fonction d'une 3ème entrée communément appelée horloge (notée CLK (clock)).
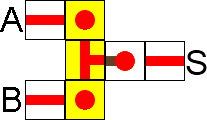
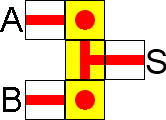
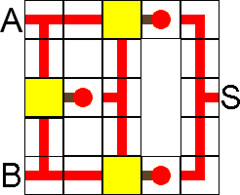
Verrou RS NON-OU
On différenciera ici le nom des entrées sorties, car contrairement aux portes précédentes on ne s'intéresse plus aux états des entrées ou sorties mais à la variation de celles-ci.
Pour la bascule Latch, on utilisera les lettres "S" (set) et "R" (Reset) pour les entrées, et "Q" et "Q" (inverse de Q), pour les sorties.
On pourra noter que contrairement aux portes logiques de base, les portes avancées ne peuvent pas être traduites sous forme de formule (on parle de bascule, et non plus de porte).
| S | R | Q | Q | |
|---|---|---|---|---|
| 1 | 1 | indéfini | indéfini | |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | conserve l'état initial | conserve l'état initial |
L'état indéfini est l'état "interdit" comme le montre le tableau, Q est l'inverse de Q en tout temps, mais dans cet état interdit, ce n'est pas toujours vrai... C'est pour cette raison que l'on n'utilise pas cet état. Activer cet état correspondrait à appuyer simultanément sur le bouton pour démarrer une machine et en même temps sur son bouton d'arrêt d'urgence...
L'utilité de la bascule réside dans le fait que l'on a une conservation de l'information de sortie.
Une activation de l'entrée "S" va faire passer la sortie Q à un état Actif (1). En repassant "S" à 0, la sortie "Q" reste activée.
Pour refaire passer "Q" à 0, il suffit d'activer l'entrée "R".
On vient donc de constituer une mémoire de 1 bit.
Les horloges / générateurs d'impulsion
Les horloges / générateurs d'impulsion
Quelque chose d'essentiel dans Minecraft pour l'automatisation des circuits est de pouvoir générer une horloge, un circuit qui génère lui-même du courant de façon régulière. C'est-à-dire qu'à un moment il y aura du courant en sortie, puis l'instant d'après il n'y en aura plus, puis il y en aura de nouveau. Tout cela sans intervention humaine.
Il est possible d'activer ou non ces circuits, vous pouvez donc les utiliser pour faire clignoter une torche si une personne est passée par là, ou faire un couloir de la mort avec des pistons sur les murs qui vont fermer le couloir sur un joueur imprudent, passez au bon moment ou c'est la mort.
Suivant le circuit choisi, la période du signal sera plus ou moins faible, le plus modulable reste l'horloge en kart. Le Rapid Pulser lui est difficilement utilisable pour activer des objets, et le 5-clock est le moins coûteux en ressource.
Une dernière recommandation : faites attention sur les serveurs, les circuits automatiques à base d'horloge peuvent provoquer des ralentissements dans la zone s'il y a beaucoup d'éléments ou de joueurs.
Le 5-clock (fréquence normale) :
Ce circuit est le plus courant quand il s'agit de faire des horloges, c'est aussi le plus simple. Il y a plusieurs versions qui existent, la différence entre elles est la place qu'elles prennent.
La version la moins utile, car prenant trop de place, sur cette capture d'écran :
Ce circuit prend 8x3x1 d'air.
En voici le schéma, même s'il est simple :
Il existe une version plus courte qui prend moins de place. La voici sur cette capture d'écran :
Ce circuit prend 10x2x1 d'air.
Voici le schéma de ce circuit :
Les répéteurs sont ici utilisés car ils ne prennent qu'un seul coté pour l'entrée, ils isolent donc les "files" de Redstone. On peut donc coller les deux lignes de blocs, contrairement à la première version.
Une dernière variante existe, bien qu'elle ne soit pas très ressemblante, mais cette dernière impose un bloc de hauteur en plus. À vous de choisir la version que vous préférez suivant la place que vous avez à disposition.
Le schéma est en deux couches.
Voici la couche du bas :
La couche du haut :
Le Rapid Pulsar (fréquence très rapide) :
Ce circuit s'utilise pour d'autres circuits, il est trop rapide pour activer des portes ou des pistons, mais il reste avant tout une horloge et il a droit à son petit paragraphe.
Voici à quoi il ressemble :
Voici le schéma associé :
L'horloge-kart (fréquence variable) :
Ce dernier type d'horloge présenté est beaucoup plus esthétique que les autres, il est également possible de bien gérer la fréquence du courant. Mais attention, vous pourrez gérer la fréquence, mais l'impulsion étant donnée par le rail, comme un bouton, le temps où le courant passera dépend du temps du bouton, qui n'est pas configurable. Il est cependant possible de régler la durée de passage du kart sur le rail, donc la période. À savoir que cette horloge ne donne pas un signal symétrique. Il peut y avoir plus de temps avec courant que sans courant, cela dépend de la taille du circuit.
En voici un qui prend peu de place, et qui peut s'utiliser pour activer des objets :
Non, pas de schéma, vous êtes grands ! Ajustez la taille du circuit, le nombre de boosters et de karts à votre envie. Pour cette taille, il faudra au moins deux rails boosters pour que le kart ne s'arrête pas.
Les commandes physiques
Il existe certaines particularités, pas forcément voulues à l'origine qui permettent d'utiliser des spécificités géométriques ou d'emplacement / de nature de bloc.
Il est ainsi possible de créer un détecteur de jour-nuit (détaillé dans l'article sur les applications de la redstone), ou bien de commander à l'eau et à la lave (malheureusement une seule fois, la machine devant être réamorcée à la main).
Pour ces deux cas, mais on ne traitera ici que du cas de l'eau et de la lave, on va profiter du fait que le calcul relatif à la redstone se fait avant le calcul des mécanismes physiques. Si bien qu'en alimentant un bloc proche d'un passage d'eau / de lave, il va être possible de bloquer l'écoulement de celle ci...
La manipulation n'est pas évidente, mais une fois le coup de main pris, ce n'est guère difficile...
Il faut tout d'abord construire le circuit, qui doit se finir sur le trajet de l'eau / la lave (seulement sur une conduite de 1 bloc de large). Le circuit devra changer d'état lorsque l'eau / la lave emporte la torche ou la poudre qui se trouve sur son écoulement. On place ensuite l'eau ou la lave dans la tranchée. Le liquide va commencer à s'écouler à partir du bloc source et va se bloquer là où a été placée la torche ou la poudre (en emportant ou brûlant celle-ci). Une inversion du signal de redstone va faire se poursuivre l'écoulement.
Une fois que le fluide s'écoule, il n'est malheureusement pas possible de l'arrêter... Il vous faut détruire la source, replacer la redstone et recommencer...
Mais à vous les joies des pièges qui inondent une salle, ou déversent des torrents de lave sur vos malheureuses proies...
À noter que la mise en place des pistons à fortement réduit l'interêt de la chose. Un mécanisme à piston peut avoir la même fonction, mais avoir l'avantage d'être réamorçable
Les tableaux de Karnaugh
À quoi ça sert ?
Le tableau de Karnaugh est l'outil par excellence pour les électroniciens en herbe. Ce tableau sert à simplifier vos circuits logiques complexes en réduisant le nombre de traitements différents. L'utilité se fait ressentir quand il y a beaucoup de configurations possibles qui amènent à un même résultat. Il existe d'autres méthodes pour simplifier des expressions, cependant, à l'aide de ce tableau nous sommes garantis de trouver une forme minimale pour vos circuits de redstone.
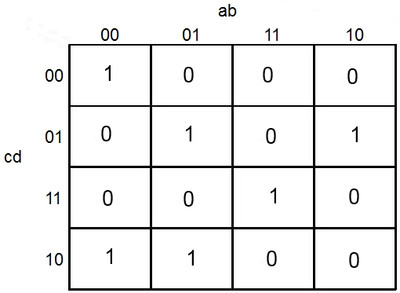
À quoi ça ressemble ?
Ne prenez pas peur, même si c'est incompréhensible !
Petite explication de ce qui est visible. Des détails seront apportés dans la partie "Comment le créer".
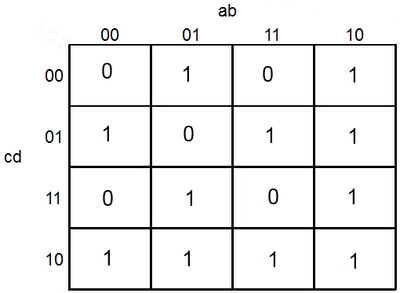
Le tableau tel qu'ici traduit le traitement voulu par le circuit de redstone, ou électrique. Les lettres, a b c d, sont les variables d'entrée du circuit et proviennent de leviers, boutons, etc. La valeur dans la case est la sortie du circuit, un 1 équivaut à du courant, un 0 équivaut au contraire.
Par exemple pour la case en bas à gauche, le tableau nous dit que il y a du courant en sortie si :
- Il n'y a pas de courant sur a.
- Il n'y a pas de courant sur b.
- Il y a du courant sur c.
- Il n'y a pas de courant sur d.
Voila pour la lecture d'un tableau. Seulement, cela sera à vous de le remplir à partir de ce que vous voulez faire.
Notation
Un circuit, il est possible d'en résumé le traitement en une ligne, qui donne pour toutes les combinaisons le résultat de la sortie. En voici un exemple :
S = a . b . c . d + a . b . c . d
Les . sont des AND, les + sont des OR. La barre signifie que la variable doit être à 0, non alimentée. Le résultat de la sortie, S, sera donc positif si :
- a n'a pas de courant, et que b, c et d sont alimentées
ou
- a et c ont du courant, et que b et d n'en ont pas
Utilité
Le but de ce tableau est de construire une expression, comme dans l'exemple de la notation, la plus simple possible. Parfois cela ne donnera rien, mais d'autres fois l'économiser en place est énorme.
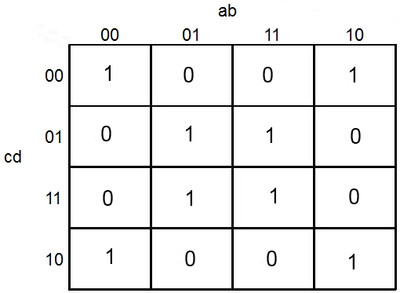
Avant de voir comment l'utiliser, nous allons voir un exemple et son résultat avec et sans cette méthode pour que vous vous rendiez compte de son utilité pratique.
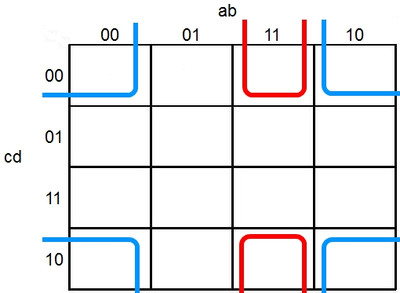
Prenez par exemple ce tableau qui peut traduire vos idées les plus folles.
Il y a huit combinaisons où l'on veut sortir du courant, les cases 1. Il est bien sûr possible d'écrire cela en prenant chaque bonne combinaison et en faisant un test dessus, on se retrouve avec huit portes OR alimentées par des AND ainsi que des inversions.
Ce qui donnerait ceci : S = a.b.c.d + a.b.c.d + a.b.c.d + ... je n'ai là que trois des huit résultats. Il est évident que cela est fastidieux et inutile.
La magie opère rapidement avec ce tableau, le résultat qui en sort sera : S = b.d + b.d.
Je vous garantie que nous avons la même chose qu'avant, mais on remplace plusieurs dizaines de portes, par cinq portes (deux inversions, deux AND, une OR) !
Comment s'en servir
Tableau de base
Dans mes exemples j'utilise quatre variables car c'est suffisant pour pouvoir montrer des choses complexes mais pas trop non plus pour avoir 50.000 termes dans l'expression. Cependant, il est possible d'utiliser autant de variables qu'on le souhaite. Vous avez peut être remarqué la construction des états dans le tableau (00, 01, 11, 10), il s'agit du code de Gray, un codage qui permet de ne changer qu'une valeur entre les différentes unités. Pour cinq variables on notera sur la ligne trois variables comme ceci : 000, 001, 011, 010, 100, 101, 111, 110 et sur les colonnes deux variables, comme ceci : 00, 01, 11, 10 pour avoir un tableau 8 x 4 cases.
Pour que vous puissiez vous adaptez à tout, voila comment il est construit. Pour passer de deux à trois variables, nous prenons 00, 01, 11, 10, qu'on écrit deux fois, sur les premiers on rajoute un 0, sur les autres un 1. Cela donne 0 00, 0 01, 0 11, 0 10, 1 00, 1 01, 1 11, 1 10.
Remplissage
Lorsque la structure du tableau est bonne, il faut encore le remplir. Cette partie est très simple, pour chaque case la question de l'état de sortie se pose, puis le résultat est à inscrire dans la case. Pour rappel : un 0 équivaut à une absence de courant, un 1 signifie la présence de celui-ci. Il peut y avoir des cas spéciaux, où l'état de sortie n'est pas important, ce cas est détaillé dans la partie "Cas particulier".
Cadre
C'est ici le cœur de la simplification ! Nous avons plusieurs 1 dans les cases, et il faut un moyen de réduire le nombre de traitement. C'est très simple. Il faut considérer le tableau dans sa globalité et réunir les résultats équivalents, les 1, pour pouvoir réduire le nombre de variables. Il s'agit en fait de les regrouper dans des carrés de 1, 2, 4, 8, 16,... valeurs identiques. Il faut en priorité faire des carrés les plus grands possibles, une valeur peut être comprise dans plusieurs carrés. Plus les carrés seront grands, moins il y aura de variables, plus l'expression sera simple. Ne vous occupez pas de la suite, faites des carrés ! Il faut que tous les 1 soient encadrés pour avoir terminé.
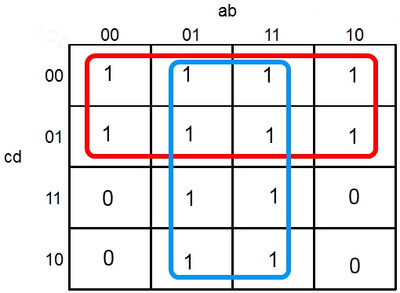
Exemple :
Résultat
Interprétons le résultat de nos cadres rouge et bleu.
Pour les traduire en expression, nous observons ce qu'ils englobent, les états des variables, et nous gardons ceux qui sont inchangés !
Pour le rouge :
- La variable « a » change dans le cadre, on ne la garde pas
- La variable « b » change dans le cadre, on ne la garde pas
- La variable « c » restent à 0 dans tout le cadre, on la garde
- La variable « d » changent dans le cadre, on ne la garde pas
Le résultat pour le cadre rouge sera c car c vaut 0. Pour le cadre bleu, le résultat sera b. Le résultat global est donc, S = b + c. Il suffit donc de tester cette petite expression pour avoir le résultat escompté.
L'exemple était très simple, et ne montre pas toutes les possibilités. Les cadres doivent être faits avec des cases adjacentes, mais il faut imaginer le tableau comme une sphère, la case en haut à gauche est reliée à celle en bas à droite !
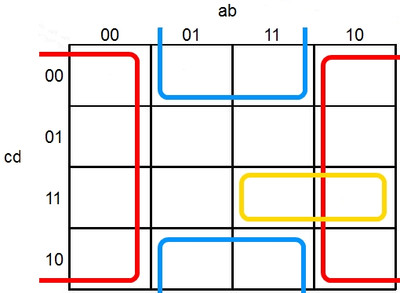
Voici des exemples de cadres possibles :
Celui-ci est très amusant, les quatre coins :
Exemple
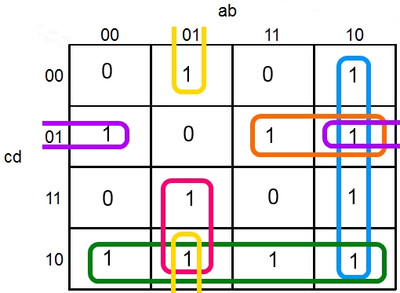
Pour finir, nous allons parler d'un exemple concret :
Ce tableau nous donne :
- Rassemblement bleu : a.b
- Rassemblement vert : c.d
- Rassemblement rouge : a.b.c
- Rassemblement orange : a.c.d
- Rassemblement jaune : a.b.d
- Rassemblement mauve : b.c.d
Voila, vous êtes aptes à simplifier vos structures !
Cas particulier :
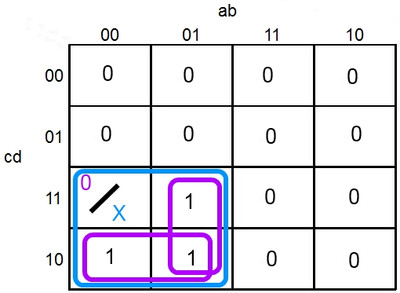
Il existe une valeur en plus, autre que 0 et 1, pour remplir le tableau. Cette valeur est un X, signifiant que l'état est indifférent ou qu'il ne se présente jamais. Nous pouvons imaginer que pour une énigme quelconque, avec des plaques de pression à différents endroits, il est impossible pour une personne de presser en même temps sur les deux plaques. Si les plaques se nomment « a » et « b », alors les cases où a=1 et b=1 n'ont aucune utilité car il est impossible d'entrer dans cette combinaison. Il est alors possible de mettre un X dans le tableau dans les cases qui font référence à cette combinaison.
La valeur X pourra faire parti d'un cadre si cela simplifie l'expression mais il n'est pas obligatoire de l'utiliser (contrairement à un 1). Voici un exemple où avec ou sans X, le résultat n'est pas le même. Nous comprenons facilement qu'identifier les cas impossibles est important.
Pour s'entraîner :
Pour vous entrainer à résoudre et optimiser vos expressions, une page wikiversité propose des petits exercices avec solutions, et s'il vous en faut davantage, cherchez simplement sur Google des exercices sur le tableau de Karnaugh.
- Usage et applications de la Redstone
- Redstone : Les bases
- Redstone : Les portes logiques
- Les pistons
- La ficelle!
Réactions
Pas de compte JeuxOnLine ?
Créer un compteQue pensez-vous de Minecraft ?
449 joliens y jouent, 680 y ont joué.
-
24 avril 2025
-
24 mars 2025
-
25 mai 2020
-
15 novembre 2018
-
13 juin 2018